The class rate is equal to the actual number of students in class divided by the number of students in class multiplied by 100%. For example, the number of applicants for a training course is 50, but in fact the number of classes is 45, and 5 people ask for leave due to the incident. Attendance rate = 45 people÷50 people*100% = 90%. In the 50-person training course, there were actually 45 people in the class, 5 people asked for leave, and the attendance rate was 90%. The above is the formula and example questions for calculating the lesson rate.

Let's change the algorithm. The arrival rate of a certain class = the actual number of people/the number of people who should arrive. The average arrival rate of all classes = The accumulation of the arrival rate of each class/The total number of classes. The advantage of this is that the number of people who should arrive in each class may be different, even so.It doesn't matter.

How should mathematics be previewed in the summer vacation of fifth and sixth grade? Are you crazy about learning ahead of time? No, that will dampen children's enthusiasm for learning and affect classroom learning next semester.The correct approach is to pay attention to the understanding of basic concepts and the mastery of basic question types. Don't worry about children learning too little. The foundation is firmly established and accumulated. After the school starts, the children's grades will rise!

 

What is the percentage?

The application of fractions and percentages is a very important content in mathematics in the sixth grade of primary school. There are three main types.：

First, find a fraction of a number, or a few percent. The second is that it is known that a few fractions or percentages of a number, find this number. Third, find that one number is a fraction or percent of the other number.

 

These concepts sound abstract, so in simple terms, what is the percentage? In fact, it is a ratio. Generally, the ratio can be 1/3 or 3/4. For example, boys account for 3/4 of the total number of students in the class, and the percentage always treats the denominator as 100 as the reference quantity. Therefore, a percentage is a ratio with a denominator of 100.

 

Typical example questions

Below we use a few typical example questions to gain a deep understanding of the percentage.

Example 1: In a shooting game, Xiao Ming shot 20 shots and scored 6 goals. What is his shooting percentage?

 

This topic is about the most basic concepts. Let's warm up first. The shooting percentage is usually converted into a percentage, that is, a percentage. Xiao Ming made a total of 20 shots, of which 6 were hit. So what percentage of all 6 shots did these 6 shots account for? Accounting for 6/20 of all.The second step is to turn the fraction into a percentage. The more direct way is to turn the denominator into 100.The numerator and denominator are multiplied by 5 at the same time, the denominator becomes 100, and the numerator becomes 30, so the percentage is 30%.

 

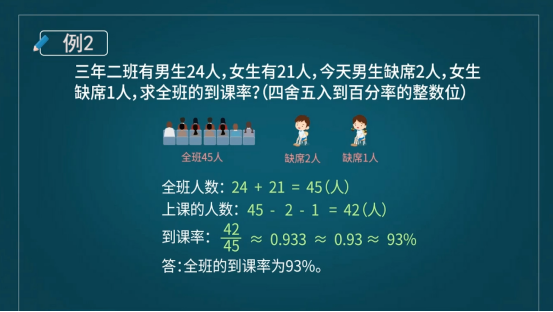
Example 2: There are 24 boys and 21 girls in the second class of the third year. Today, there are 2 boys absent and 1 girl absent. What is the attendance rate of the whole class? (Rounded to the integer digit of the percentage)

 

The attendance rate refers to the ratio of the total number of people in the class to the total number of people in the class, usually expressed as a percentage. How many people are there in the class? There are 24 boys and 21 girls, adding up to 45 people. How many people are in class? There are 2 boys absent and 1 girl absent. Then there are 45-2-1=42 (people) who actually came to class today. So the arrival rate is 42/45.

The second step to turn the fraction into a percentage is to change the denominator from 45 to 100, which is slightly troublesome if it cannot be divisible by.At this time, another method can be considered, which is to turn it into a decimal.Dividing 42 by 45, which is approximately equal to 0.93333, is inexhaustible and is a cyclic decimal. Therefore, such topics usually require us to round to the second decimal point, which is the integer of the percentage.Usually we still have to divide by one more digit before we can round it, that is, we have to count to the third place after the decimal point. After rounding, it is finally 0.93, which is 93%.Today's attendance rate reached 93%.

 

Through Example 1 and Example 2, it can be found that there are two different calculation methods for the percentage. The first can directly change the denominator to 100, then the denominator can usually be changed to 100 by simple multiplication and division. Second, for those whose denominator is not easy to become 100, you can use division to turn it into a decimal to deal with it.

 

Example 3: 1 kilogram of sugar water contains 250 grams of sugar. What percentage of sugar is in the sugar water?

 

Sugar in sugar water accounts for a few percent of all sugar, that is, the weight of sugar accounts for a few percent of all weight.

What is the total weight? The title tells us that it is 1 kilogram, which is 1000 grams. What is the weight of sugar? 250 grams. So what percentage of 1000 grams does 250 grams account for? Use the score to calculate it, you know that 250/1000 is approximately divided by 10, and the final calculation is 25/100, which is 25%. So sugar accounts for 25% of sugar water.

 

Example 4: The figure shows the statistical table of poultry in a farmhouse. Please calculate the percentage according to the types of various types of poultry.

 

This is a question that needs to be calculated by reading a picture. First, calculate the number of chickens as a percentage of the total. Divide the number of chickens by the total number, 40/80, which is simplified to 1/2, which is 50%. Consider ducks in the same step. There are 24 ducks, 24/80, which is 30%. The same goes for the remaining “others", 16/80, which is equal to 20%.

 

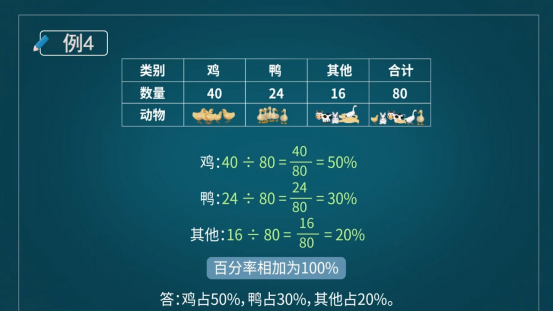
Did everyone find out? The sum of these three percentages plus 50%+30%+20% is 100%. This is very important. When you study statistics in junior high school, you will slowly understand why and must be 100%. If you use a histogram or pie chart to represent it, you can intuitively see the percentage of each type of poultry in the total.

 

This kind of statistical graph reading topic has become popular in recent years, in the form of bar charts, pie charts, etc., So the ability to read and draw diagrams is also very important. You can feel it through this example question.

summary

The topics we are talking about today are very basic, but don't underestimate these most basic knowledge. The topic of percentages is a very important knowledge point from elementary school to middle school to high school. Children will use it in the future to study physics, chemistry and other subjects. Let's start with this article first. The knowledge of percentages has more in-depth applications in subsequent topics such as the application of percentages, concentration issues, and discounts in business. This is a process from shallow to deep. We must lay a solid foundation.